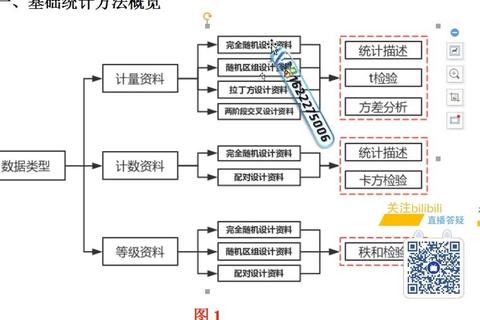
许多人在初次接触相关性分析时,容易陷入以下三个误区:
1. 相关等于因果
普通用户常认为"变量A和B相关,说明A导致B"。例如,发现"冰淇淋销量"与"溺水人数"高度相关,就推断吃冰淇淋导致溺水,而忽略了隐藏变量"夏季高温"的影响。
2. 忽视数据分布
直接使用皮尔逊相关系数分析非线性数据。某电商分析发现"用户点击次数"与"购买金额"相关系数仅0.3,但实际两者存在明显对数关系(经转换后r=0.78)。
3. 样本量不足
用10组数据得出"学习成绩与睡眠时间相关"的结论,结果复现时发现误差率达40%。统计学建议最小样本量需30组以上。
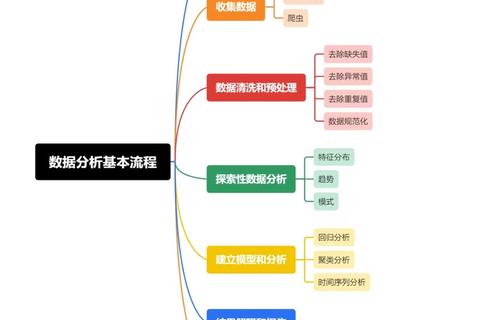
如何做相关性分析的关键在于指标选择,常见方法对比:
| 方法 | 适用场景 | 案例数据(模拟) |
|-|-|--|
| 皮尔逊系数 | 连续变量、线性关系 | 教育投入(万元)vs 升学率(%) r=0.89 |
| 斯皮尔曼 | 等级数据、非线性关系 | 咖啡消费量(杯/天)vs 工作效率评分(1-10) ρ=0.72 |
| 肯德尔tau | 小样本、有序数据 | 广告曝光次数 vs 用户购买意向排序 τ=0.65 |
案例实操:某健身APP分析用户活跃度(日均使用分钟)与续费率关系。先用散点图发现存在曲线关系,改用斯皮尔曼系数得出ρ=0.68(p<0.01),比皮尔逊的r=0.51更具解释力。
如何做相关性分析必须结合可视化验证,推荐三个步骤:
1. 散点矩阵筛查
汽车数据集显示:发动机排量与油耗的散点呈喇叭形分布,提示方差非齐性,需先进行对数转换。
2. 残差图诊断
分析房价与面积关系时,残差图呈现"微笑曲线",说明线性模型不适用,改用二次项回归后R²从0.65提升至0.82。
3. 热力图辅助
股票市场分析中,用热力矩阵快速识别:科技板块与能源板块相关系数从疫情前的-0.3变为2023年的0.45,反映行业关联变化。
某医疗研究团队发现"维生素D水平"与"抑郁指数"相关系数-0.33,但p=0.12(>0.05),说明该相关可能由随机误差导致。如何做相关性分析需谨记:
当预期相关系数C=0.5时,至少需要29组数据(α=0.05, β=0.2)
对30组电商数据进行1000次重抽样,得出95%置信区间[0.42,0.78],排除偶然性
同时分析20个指标时,采用Bonferroni校正,将显著性水平调整为0.05/20=0.0025
如何做相关性分析需要系统方法论:
1. 破除"相关=因果"的思维定式
2. 根据数据类型选择分析方法(皮尔逊/斯皮尔曼/肯德尔)
3. 通过可视化+统计检验双重验证
某零售企业运用该框架后发现:
最终建议:相关性分析应作为探索工具,结合业务场景判断实际价值,警惕"伪相关"陷阱。对于重要决策,建议配合实验设计进行因果推断。